ellipticnews

New cryptanalysis of M-SIDH isogeny cryptography

Posted on October 4, 2023 by ellipticnews

This post is about the paper A polynomial time attack on instances of M-SIDH and FESTA by Wouter Castryck and Frederik Vercauteren.

As we all know, SIDH was broken in 2022 by using knowledge of exact images of torsion points under a secret isogeny. (For more details, see previous blog post, and another, and Quanta article.) Precisely, in SIDH the secret isogeny $\phi : E_0 \to E_1$ has known degree $A$ , and one is given $\phi(P), \phi(Q) \in E_1$ where $P, Q$ are a basis for $E_0[B]$ . Here $\gcd(A,B) = 1.$ The key technique is a result from Kani, which involves isogenies of Abelian varieties of dimension more than one.

In response, several papers proposed ways to fix it by “blinding” the images of the torsion points and/or the degree of the isogeny $\phi$ . The M-SIDH paper proposed to hide the degree of $\phi$ and to blind the points as $S = \lambda \phi(P), T = \lambda \phi(Q)$ for some secret $\lambda$ that squares to one modulo $B$ . FESTA is a bit more general, and I won’t talk about it in detail here.

Sections 4.2 and 4.3 of the M-SIDH paper show an attack on the scheme for special curves $E_0$ using “lollipop” maps (see below). Section 5 of the M-SIDH paper explains that hiding the degree adds no security, in the sense that one can reduce the problem to a case of known degree. Hence whatever is the security, it is coming from the fact that $\lambda$ is unknown to an attacker.

The reason why exact knowledge of the torsion is needed for the SIDH attacks is because these attacks set up an isogeny $F$ of Abelian varieties that is defined by an explicit kernel subgroup in terms of $\phi(P), \phi(Q)$ and also the exact images of $P, Q$ under some other (known) isogeny. When given only $\lambda \phi(P), \lambda \phi(Q)$ the kernel is wrong and the isogeny $F$ is not the desired map (indeed, it may not even be an isogeny of polarized abelian varieties). So it was plausible that M-SIDH and FESTA might resist attack.

Castryck and Vercauteren show a more general attack strategy on these proposals than considered in the previous works. The paper builds on the well-known idea of “lollipops” (the terminology was introduced in this paper by de Quehen, Kutas, Leonardi, Martindale, Panny, Petit, and Stange). In isogeny crypto a lollipop is formed by taking an isogeny from one curve $E$ to another curve $E_0$ , applying an endomorphism on $E_0$ , and then applying the dual map back to the original curve $E$ , so that the whole composition is cyclic. See the picture below from the paper linked above. Be warned that lollipops are not as sweet as they sound!

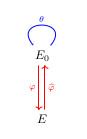
The obvious idea is to try to do a Kani-type attack on the isogeny $\phi : E_0 \to E_1$ , but this seems to be prevented by the blinding. The clever idea is to do Kani-type attack on a different isogeny $\psi : E_1 \to E_1^{(p)}$ which uses the images of the blinded points $S, T$ rather than the original points on $E_0$ . The map $\psi$ is a sort-of lollipop map with $\phi$ , but one can also evaluate it (up to known scalar multiple) as the Frobenius map. Hence one can compute $\psi(S), \psi(T)$ . Knowing these points, one can mount the Kani-type attack and learn $\psi$ .

We present one of the cases that is handled in the paper. Suppose that $E_0$ is defined over $\mathbb{F}_p$ . We have $E_1$ and want to compute the unknown map $\phi : E_0 \to E_1$ . Suppose that $\phi$ is not defined over $\mathbb{F}_p$ . Consider the Frobenius maps $\sigma_1 : E_1 \to E_1'$ and $\sigma_0 : E_0 \to E_0$ . Let $\phi' : E_0 \to E_1'$ be the “pushforward” of the unknown map $\phi$ , which is just the Frobenius conjugate of $\phi$ . We have $\phi' \circ \sigma_0 = \sigma_1 \circ \phi$ . We don’t know $\phi$ or $\phi'$ , but we can consider the composition, where $\hat{\phi}$ denotes the dual isogeny,

$\psi = \phi' \circ \hat{\phi} .$

Note that the degree of $\psi$ is $A^2$ . Further, we generally expect $\psi$ to be cyclic, since for $R \in E_1[A]$ we have $\hat{\phi}(R) \in ker( \phi )$ which is not usually equal to $ker( \phi' ) = \sigma_0( ker( \phi ))$ .

The key result is Lemma 3 of the paper. Let $S = \lambda \phi(P), T = \lambda \phi(Q) \in E_1$ . Let $S' = \sigma_1(S), T' = \sigma_1(T) \in E_1'$ , which an attacker can compute. The lemma shows that from these points one can determine $\psi(S), \psi(T)$ exactly. I emphasise the main point: the scalar multiplications by $\lambda$ somehow don’t matter, as we are directly attacking the points $S, T$ . To finish the attack, one runs the previous SIDH attack on $\psi$ , using Kani’s technique, to learn it completely. Finally, evaluate the isogeny on points of order $A$ to learn $\phi$ (since $\psi$ is cyclic we can expect to learn the kernel we desire).

This gives an attack on M-SIDH when the starting curve $E_0$ is defined over $\mathbb{F}_p$ . The paper shows a more general attack that covers some more special cases of $E_0$ . The general case of M-SIDH is not yet broken, but the paper discusses some strategies (and defenses) against a malicious party installing a backdoor in $E_0$ .

The paper then studies a special case of FESTA, which is not proposed in the FESTA paper, and shows an attack. The paper says “FESTA with overstretched parameters is insecure”. But I believe no proposed case of FESTA is broken by this paper. The paper remarks that “similar information” is leaked in CSIDH, since $\phi$ maps the eigenspaces of Frobenius on $E_0$ to the corresponding eigenspaces on $E$ . However, there is no efficient attack known on CSIDH either. More generally, the information you get for free from an orientation does not seem to lead to any new attack.

While on the subject of CSIDH, these papers also do not break CSIDH:

The supersingular Endomorphism Ring and One Endomorphism problems are equivalent by Aurel Page and Benjamin Wesolowski.
The supersingular endomorphism ring problem given one endomorphism” by Arthur Herlédan Le Merdy and Benjamin Wesolowski.

Both papers are about knowledge of one endomorphism. The first shows that if one can generate one endomorphism for any random supersingular curve, then there is an efficient algorithm to compute the endomorphism ring (and hence solve isogeny problems) for any fixed supersingular curve. It sounds like this would break CSIDH, since in CSIDH we do know one endomorphism. But that’s not how the algorithm works. The idea is to take a target curve $E$ and generate random isogenous curves $E'$ , find an endomorphism on each curve $E'$ , and then pull these endomorphisms back to $E$ . This then allows to compute $End(E)$ . But the one known endomorphism on every CSIDH curve does not allow to make this approach work. The second paper is about extending the known attacks on CSIDH to other curves, and it does not change the current understanding of the security of CSIDH.

What can we conclude from this about the security of fixes to SIDH, such as M-SIDH and FESTA? My personal opinion is that it seems unlikely that such simple tweaks to SIDH are enough to be secure. But I await more research to understand this better. On the other hand, CSIDH continues to withstand scrutiny by cryptanalysts, and no attacks are known that are better than the well-known subexponential-quantum-time Kuperberg algorithm.

— Steven Galbraith

Posted in Uncategorized | Leave a comment

SIAM Conference on Applied Algebraic Geometry (AG23)

Posted on July 20, 2023 by ellipticnews

The SIAM conference on Applied Algebraic Geometry took place in Eindhoven last week.

The “mini symposia” included:

Applications of Algebraic Geometry to Post-Quantum Cryptology
Elliptic Curves and Pairings in Cryptography
Applications of Isogenies in Cryptography

Despite having promised myself to attend talks outside of my domain, I ended up attending all the talks in the “Applications of Algebraic Geometry to Post-Quantum Cryptology” mini-symposium. The first day was mostly about multi-variate crypto. Bo-Yin Yang gave two talks about the recent history of attacks on multivariate schemes, and some insights into the new UOV and TUOV submissions to NIST’s on-ramp signature call. The rest of the talks was about cryptanalysis. The day was closed by something more palatable to the audience of this blog and my personal highlight of the conference: Guido Lido took over Giulio Codogni’s spot and delivered a spectacular double talk on the spectral properties of isogeny graphs with level structure. At Eurocrypt, Guido and coauthors had shown that supersingular isogeny graphs with Borel level structure are Ramanujan, and applied this to construct statistically zero-knowledge proofs of isogeny knowledge. Here Guido and Giulio generalize the result to arbitrary level structures, showing that, modulo an obstruction coming from the Weil pairing, they are all “somewhat Ramanujan”. Guido barely said “crypto”, mistook the audience for the SGA seminar, and took us along in a journey through modular curves and Hecke operators that was easily the most AG talk in SIAM AG!

The second day was nearly all isogenies, and very much Italian. I essentially remade Guido’s talk for the layman, presenting along the way a still unpublished attack against “SIDH with a single torsion point”. Federico Pintore followed up with hard facts and numbers on still-unbroken SIDH-like signatures: nothing NIST-worthy, but some good cleanup. Annamaria Iezzi presented some progress on computing the endomorphism ring of supersingular curves: nothing new complexity-wise, but some heuristics are removed. Unfortunately I missed Valerie Gilchrist’s talk on supsersingularity testing. Thomas Decru presented his attack on SIDH, I don’t suppose the readers of this blog need to know more about this. Boris Fouotsa presented some counter-measures against the SIDH attacks that appeared at the last Eurocrypt, and then presented some nice improvements using what he calls “artificial orientations” (which, by the end of the symposium, everyone understood as being nothing else than Cartan level structures). Wouter Castryck gave the only non-isogeny talk of the day: he presented an attack against a key-exchange scheme based on “disguised” Veronese varieties, that one would be tempted to classify into the multi-variate bucket. The attack uses what Wouter calls “the Lie algebra method”; as he puts it: it’s all linear algebra, although quite advanced one.

The audience of the blog would certainly have found the workshop “Elliptic Curves and Pairing in Cryptography” interesting, however I attended other workshops, so I cannot report on it.

The week was closed by the well attended “Applications of Isogenies in Cryptography” workshop. The quick summary is: 50% SQIsign, 50% isogenies of abelian surfaces, and a vanishingly small set of other stuff.

Michael Meyer presented the state of the art on generating SQIsign-friendly primes and reported on the searches that have been run for the current NIST submission. Lorenz Panny and Antonin Leroux gave nice presentations on the effective Deuring correspondence, both in the general case and in the specific case of SQIsign. When asked how optimistic he is about SQIsign’s potential for standardization, Antonin gave a pretty pessimistic answer. Benjamin Wesolowski came to the rescue giving the audience some hope back with his presentation on SQIsignHD, the SIDH-attacks-based variant of SQIsign that promises much simpler and faster (and slightly shorter) signatures at the cost of a considerably more complex verification. Gustavo Banegas explained how to implement all of this in (maybe) constant time. Continuing on the “using SIDH attacks for good” topic, we had talks by Giacomo Pope on algorithms for computing isogenies between products of elliptic curves, and by Luciano Maino on using the SIDH attacks for making a PKE scheme named FESTA.

In the vanishingly small set, Peter Kutas gave a nice talk on a quantum break of pSIDH, an obscure (and totally impractical) key exchange that had always looked too risky to be true. More than by the breaking of pSIDH, I was impressed by the underlying technique. In past work, Peter and coauthors had defined a group action of GL₂ on the set of j-invariants at a certain distance from a starting curve, and used that to give a subexponential quantum attack (essentially, Kuperberg) on overstretched variants of SIDH. I wasn’t impressed at the time, given that we already had classical attacks on overstretched SIDH. What’s new is that Peter & co. found a way to express the problem of breaking pSIDH as a hidden subgroup problem, where the ambient group is GL₂ and the hidden subgroup is a Borel subgroup. By sheer coincidence, this non-abelian HSP turns out to be solvable in quantum polynomial time! Interestingly, the same idea would apply to SIDH and M-SIDH too if only they contained enough torsion point information (pSIDH contains an arbitrary amount of torsion point information, and seems to have been invented on purpose to make this attack possible!). To me, this is a strong indication that M-SIDH should be set up with a starting curve of unknown endomorphism ring.

For a change of scenery, Ward Beullens presented his attacks on signature schemes based on alternating trilinear forms. The only connection with isogenies seems to be the appearance of nice volcano-like graphs when studying the case of dimension 9 (one among many parameter sets), however the explanation appears to have more to do with an abelian surface acting on some bilinear forms.

But all of the above can be easily found on eprint, and the audience of the blog was probably already familiar with many of the results. The surprise of the workshop were the talks by David Kohel and Chloe Martindale. Both reported on work in progress and in both cases the audience was left with a feeling that, despite the beautiful theory, some fundamental ingredient is still missing.

David talked about formal orientations of elliptic curves. In the spirit of his and Leonardo Colò’s pioneering work on orienting supersingular elliptic curves, they are now trying to give a sense to, and possibly make cryptography out of, attaching some endomorphism ring information to the formal group of an elliptic curve. The algebra looks quite different from what we have been used to so far, as there is essentially a unique endomorphism ring for all curves. David concluded on a rather disconsolate note, arguing that all useful information seems to be extremely hard to compute.

Chloe presented ideas about recasting SQIsign in the framework of Bruhat-Tits trees. Although most of it is about using different terminology for the same objects that appear in the Deuring correspondence, her hope is to push much of the complexity of SQIsign into the key generation, making signing blazing fast. However, she and Ross Bowden appear to be stuck at some lattice problem that would let them describe the way the Bruhat-Tits tree folds, and sent a cry for help.

Overall, SIAM AG was intense and fun, remaining one of my favorite conferences. There exist video recordings of all the sessions, and you may get a hand on them if you ask the speakers politely (I don’t think we were asked for authorization to publish, so I don’t expect them to ever become available on youtube, unfortunately).

— Luca De Feo

Posted in Uncategorized | 1 Comment

Some comments on the CSIDH group action

Posted on May 15, 2023 by ellipticnews

Lorenz Panny recently wrote a detailed and interesting blog post with the title CSI‑FiSh really isn’t polynomial‑time. The purpose of this post is to give some more context and discussion, and mention some recent papers.

CSIDH is an isogeny-based primitive. It is not affected by the attacks on SIDH, so is currently believed to be secure. It is an implementation of a cryptographic group action. For a prime $p$ , the group $G$ is the ideal class group of the quadratic field $\mathbb{Q}(\sqrt{-p})$ , and the group acts on the set $\mathcal{X}$ of supersingular elliptic curves with $j$ -invariant in the finite field $\mathbb{F}_p$ .

By the way, I have recently posted a short note giving an elementary presentation of the math behind CSIDH and the action $a*E$ . I hope readers will enjoy some of the constructive and simple proofs in the note.

We denote the abelian group action by $*$ . There is a natural analogue of the Discrete Logarithm problem: Given $E \in \mathcal{X}$ and $a*E$ to compute $a \in G$ . There is also an analogue of the Diffie-Hellman problem: Given $E , a*E, b*E$ to compute $(ab)*E$ . If this problem is hard then we have a Diffie-Hellman protocol as follows: Alice chooses $a \in G$ and sends $a*E$ to Bob. Bob chooses $b \in G$ and sends $b*E$ to Alice. Then both of them can compute $(ab)*E$ but it is conjectured that an attacker cannot compute this value.

Unfortunately, CSIDH does not provide a perfect group action as we would like. This is discussed in detail in the paper Cryptographic Group Actions and Applications by Alamati, De Feo, Montgomery, and Patranabis. I will call this [ADFMP].

The paper [ADFMP] defines the notions of effective group action (EGA) and restricted effective group action (REGA). In short, we ideally want EGA (which allows to efficiently compute $g * E$ for uniformly sampled $g \in G$ ) but from CSIDH we get REGA (which allows to efficiently compute $g * E$ only for some $g \in G$ ).

When doing key exchange this is not much of a problem, as one can choose a key space smaller than the whole of $G$ . A recent paper Low Memory Attacks on Small Key CSIDH by Chi-Domínguez, Esser, Kunzweiler, and May analyses the security of CSIDH when using a small subset of $G$ . The paper is nice: it shows how some ideas from coding theory (specifically, information-set decoding) are relevant to isogeny crypto.

The problem arises when doing digital signatures, or other protocols that need uniform elements in $G$ for the security proof to work. For this one needs an EGA and the only way we know how to do this is to compute the class group structure. Such signature schemes for group actions go back to Couveignes and Stolbunov. The state-of-the-art for CSIDH signatures is the work of Beullens, Kleinjung, and Vercauteren [BKV] CSI-FiSh: Efficient isogeny based signatures through class group computations. The CSI-FiSh paper computes the class group structure for an instance of CSIDH with 512-bit prime. The class group has size approx $2^{257.136}$ . Knowing the class group structure one has an EGA and a secure signature scheme. (This blog post is about CSIDH, so I do not mention SQISign.)

However, this is just a single instance, and the class group for 512-bit CSIDH is generally considered to be too small to resist a full quantum attack using Kuperberg’s algorithm. For high security levels we need to be able to compute with larger class groups.

Asymptotically, to resist Kuperberg’s quantum algorithm we want the class group to have size $2^{\lambda^2}$ , where $\lambda$ is the security parameter. So we should work with elliptic curves over a field of size $p \approx 2^{2\lambda^2}$ . (These choices may be excessively large, but they are a conservative choice.)

There are two issues with getting an EGA from CSIDH. The first problem is to compute the size and structure of the class group. This can be done in quantum polynomial time. The recent SCALLOP paper by Fouotsa, Kutas, Leroux, Merz, Panny and Wesolowski [FKLMPW] is about this first issue in the classical case. The second problem arises because efficiently computing $g \in G$ requires solving a close vector problem in a lattice to within a polynomial factor. This is hard, even for quantum computers. Some asymptotics are discussed in the full version of [ADFMP], where they argue that an exponential pre-computation may allow the group action to be efficiently computed. But Panny’s recent blog post argues that this is not realistic. Essentially, he notes that it doesn’t make sense for the precomputation cost to exceed the attack cost on the system.

Due to this lattice problem, currently one cannot view CSI-FiSh as a signature scheme in the formal sense (namely as a triple of algorithms, KeyGen, Sign, Verify that run in polynomial-time in the security parameter, even if one allows KeyGen and Sign to be quantum algorithms).

However, all hope is not lost! The SeaSign protocol by De Feo and I does not suffer from these issues. We do not need an EGA. We show how to get a secure signature scheme where the running time of all algorithms scales polynomially in the security parameter.

Precisely we propose using $\lambda$ distinct small primes of size $\lambda \log(\lambda)$ , $p \approx 2^{2 \lambda^2}$ , and exponents of size $O( \lambda^2 )$ . Giving total complexity $\tilde{O}( \lambda^4 )$ operations in $\mathbb{F_p}$ , which is $\tilde{O}( \lambda^6 )$ bit operations for one group action. The total sign/verify time for SeaSign is $\tilde{O}( \lambda^7 )$ bit operations, since the protocol has to be repeated $\lambda$ times.

Of course, “polynomial-time” and “practical” are not the same thing. It is an interesting problem to work out what is best for actual practical implementations at high security level. At the moment, the approach in the SCALLOP paper may be the best way to go. As observed in that paper “the lattice rank tends to be relatively small, letting us compute a nearly optimal basis in negligible time”. But I note that the largest example in the SCALLOP paper is only a 512-bit class group (and 75-dimensional lattice), which may not be large enough for high security applications.

— Steven Galbraith

Posted in Uncategorized | Leave a comment

Equivalence between CDH and DLP

Posted on April 19, 2023 by ellipticnews

(Apologies I wrote this quickly and there may be typos.)

The paper Dlog is Practically as Hard (or Easy) as DH – Solving Dlogs via DH Oracles on EC Standards by Alexander May and Carl Richard Theodor Schneider seems to have caused some excitement and anxiety, so I thought I would write a quick explainer about what it means.

This is a nice paper. But it is important to point out two facts:

It does not fundamentally change our understanding of CDH and DLP.
It does not lead to a new attack on any real-world system.

Let me briefly explain.

Overview of the moral equivalence of CDH and DLP

Let $P$ be a point on an elliptic curve of prime order $r$ . The Computational Diffie-Hellman (CDH) problem is: Given points $(P, [a]P, [b]P)$ to compute $[ab]P$ . This computational assumption underlies many elliptic curve cryptosystems, especially those based on key exchange or encryption.

Obviously if you can compute discrete logs (ie solve DLP) then you can compute $[ab]P$ . If you play around with CDH for a while you start to convince yourself of the “moral truth” that the only way to solve CDH is to compute DLP. In short, one may start to believe that the computational problems CDH and DLP may be equivalent.

Wonderfully, this equivalence has been formalised. There are algorithms to solve DLP if given access to an oracle that solves CDH. The basic idea is due to den Boer (CRYPTO 1988) for CDH in a group of order $r$ by working in an “auxiliary group” $\mathbb{F}_r^*$ . The idea was further developed by Maurer (CRYPTO 1994), who replaced the “auxiliary group” with an elliptic curve over $\mathbb{F}_r$ . Further refinements were done by Maurer and Wolf (CRYPTO 1996, SIAM J. Comput. 1999) and Muzereau-Smart-Vercauteren (LMS J. Comput. Math. 2004), Bentahar (IMA Cryptography and Coding 2005).

The core of these methods is to perform computations with the auxiliary group “in the exponent”. So one needs to do additions and multiplications modulo $r$ . Additions are easy: Given $[a]P$ and $[b]P$ one adds the points to compute $[a+b]P$ . Multiplications are hard: Given $[a]P$ and $[b]P$ we need to compute $[ab]P$ , and this is provided by the CDH oracle. The whole point is to be able to do these operations without necessarily knowing what $a$ and $b$ are. I refer you to Chapter 21 of my book for all the gory details (and references to the papers mentioned).

I want to stress that the algorithms do things like “square-and-multiply” in the exponent. Suppose I want to compute $[a^n]P$ from $[a]P$ . Then I can call the CDH oracle on $([a]P,[a]P)$ to get $[a^2]P$ . Then I can call the CDH oracle again on $([a^2]P,[a^2]P)$ to get $[a^4]P$ etc. I need the CDH oracle to work on any chosen inputs

I just said “there are algorithms to solve DLP if given access to an oracle that solves CDH”. But I didn’t say if they are efficient algorithms or not! This depends on the auxiliary curve. In theory, to get a polynomial-time algorithm it is necessary to have an auxiliary curve of polynomially-smooth order. But asymptotic security is a bit awkward for such questions so it is more common to make concrete estimates/calculations for specific instances. It is conjectured that suitable auxiliary curves exist. For each prime $r$ one just needs a single nice auxiliary curve. Hence, for theoretical people like me, the “moral truth” that CDH is equivalent to DLP is established.

For practical people the problem is how to generate such nice curves. Some work on this problem was done by Muzereau-Smart-Vercauteren and Bentahar. The recent eprint paper is on this part of the task. They generate a bunch of nice auxiliary curves. It means that even practical people can believe the moral truth that CDH and DLP are equivalent for certain elliptic curve groups of interest. I like the paper. It is good work. The purpose of this blog post is not to criticise those authors. The purpose is to explain the impact of the work.

Back to the two facts I started with: The new paper does not fundamentally change our understanding of CDH and DLP, because the moral truth that CDH and DLP are equivalent was already clear. But how can I be sure the new paper does not lead to an attack on any real-world system?

How can I be certain the paper does not lead to an attack on any real-world system?

Suppose a developer accidently created a system that provides a CDH oracle to an attacker. How did they do that? They must have somehow written a program that solves CDH in general. This means (because of the “moral truth” we have been talking about) that this developer accidently and unwittingly wrote a program that computes discrete logarithms on elliptic curves. I consider it unlikely that someone could do that. (This is an understatement.)

What types of oracles are provided by real-world systems?

I believe there are real-world systems that provide certain types of CDH oracle. I have not had time to look into this, but usually these are some kind of static-Diffie-Hellman oracle. Such oracles have a secret $s$ , and on input a point $P$ they compute $[s]P$ . One big difference between such oracles and a general CDH oracle is that I know how to implement such an oracle without solving DLP first.

There are improved algorithms for DLP given such an oracle, due to Brown-Gallant and Cheon. They are explained in Section 21.5 of my book. It is important to stress that these may be better than solving the DLP using Pollard rho, but they are still exponential-time algorithms. If your system is providing an attacker with a static-Diffie-Hellman oracle then you should check your instance meets the required security level.

There are also all sorts of variants of CDH like one-more Diﬀie–Hellman problems, but I don’t have time to talk about them. If I had time, I’d also love to tell you about how pairing inversion provides a CDH oracle, but I’ll just refer you to Verheul (“Evidence that XTR is more secure than supersingular elliptic curve cryptosystems”, J. Crypt. 2004), and Galbraith-Hess-Vercauteren (“Aspects of Pairing Inversion”, IEEE Trans IT 2008).

— Steven Galbraith

PS. There might be bad implementations or bad cryptosystems in the real world that provide an attacker with an oracle that allows them to break the cryptosystem. But that’s nothing to do with the recent eprint paper either. So this would not contradict the two facts I stated above.

Posted in Uncategorized | 3 Comments

EdDSA standardized

Posted on February 6, 2023 by ellipticnews

A new version of the NIST Federal Information Processing Standard (FIPS) for Digital Signatures has been published. Also see here.

This version includes EdDSA. There are (at least) two notable features of EdDSA. First, it is more closely related to Schnorr signatures than ECDSA. This means it avoids (in my opinion) many of the clunky aspects of ECDSA and allows a much more elegant security analysis. Second, it uses curves in Edwards form. Specifically, the document Recommendations for Discrete Logarithm-based Cryptography: Elliptic Curve Domain Parameters states “this Recommendation includes two newly specified Edwards curves, which provide increased performance, side-channel resistance, and simpler implementation when compared to traditional curves”. The curves include the widely used Edwards25519 curve.

I also take the opportunity to advertise this page which lists applications that use Ed25519.

— Steven Galbraith

Posted in Uncategorized | Leave a comment

Attacks on SIDH/SIKE

Posted on August 12, 2022 by ellipticnews

You may feel like you are having trouble keeping up with the news on SIDH/SIKE. So am I! I hope this blog post doesn’t instantly become obsolete due to new advances.

To recall, there are now three preprints giving attacks on SIDH:

An efficient key recovery attack on SIDH (preliminary version) by Wouter Castryck and Thomas Decru. Posted July 30.
An attack on SIDH with arbitrary starting curve by Luciano Maino and Chloe Martindale. Posted August 8.
Breaking SIDH in polynomial time by Damien Robert. Posted August 10.

The first two are parallel independent works that apply a theorem due to Kani to break SIDH in some special cases. One of the special cases was the NIST submission SIKE, meaning that SIKE was able to be broken easily on a laptop. The most recent paper by Damien Robert is influenced by the previous two works, and extends the attack to work in a much more general case. This now breaks SIDH completely in all cases.

I will summarise Damien Robert’s work below, but first a few other updates.

I put up a note Kani for beginners to explain in an elementary way that Kani’s “isogeny diamonds” are the same as SIDH squares, and to give some intuition for what Kani’s theorem says.
Rémy Oudompheng posted A note on implementing direct isogeny determination in the Castryck-Decru SIKE attack and Benjamin Wesolowski posted Understanding and improving the Castryck-Decru attack on SIDH . Both notes explain an improvement to the attack. The main idea seems also to have been had by Christophe Petit and Maino-Martindale.
The sage code has been updated with these techniques, allowing it to break some instances in under a minute.
Tomoki Moriya has posted https://eprint.iacr.org/2022/1019, which gives a possible fix for SIDH. Much less efficient and practical though.

Now to sketch the idea by Damien Robert. For consistency with my previous blog post I use some of the Castryck-Decru notation.

Recall that in SIDH we have a base curve $E_0$ and isogenies $\phi_A : E_0 \to E_A$ of degree $2^a$ and $\phi_B : E_0 \to E_B$ of degree $3^b$ , together with some auxiliary points. Assume $2^a > 3^b$ .

The most natural way to break SIDH is to compute $\phi_B$ on points of order $3^b$ , from which one can then determine $\ker( \phi_B )$ and SIDH is broken. (This is the goal of the torsion-point attacks by Petit et al, it is also the idea for the improvement to the original attack by Rémy Oudompheng and others that I mentioned above.) This is what Damien Robert’s attack does too.

Let $c = 2^a - 3^b$ . Then we can write $c$ as a sum of four squares. In this post I will take the simpler case when all prime factors of the square-free part of $c$ are congruent to 1 modulo 4, in which case we can write $c = a_1^2 + a_2^2$ where $a_1, a_2$ are integers. [Note added 15/8/2022 thanks to Daniel Bernstein: To do this we need to factor $c$ , which is polynomial-time for quantum computers or subexponential-time classically. The 4 squares case is polynomial-time classically.] Let $M = (\begin{matrix} a_1 & a_2 \\ -a_2 & a_1 \end{matrix})$ . Then $M^t M = (a_1^2 + a_2^2) I_2 = c I_2$ where $I_2$ is the $2 \times 2$ identity matrix. Hence $M$ defines an isogeny $\alpha : E^2 \to E^2$ for any elliptic curve $E$ . Specifically $\alpha(X,Y) = ( [a_1]X + [a_2]Y, [-a_2]X + [a_1] Y )$ . The dual isogeny $\hat{\alpha}$ corresponds to the transpose $M^t$ . We have $\hat{\alpha}\alpha = [c]$ as a map from $E^2$ to itself. We will apply this map to both $E_0$ and $E_B$ .

The secret isogeny is $\phi_B : E_0 \to E_B$ and we can extend this to a map from $E_0^2 \to E_B^2$ as $\phi_B( X, Y ) = ( \phi_B( X ), \phi_B( Y ) )$ . Note that $\phi_B$ commutes with $\alpha$ , since $\phi_B$ is a group homomorphism.

We can define an isogeny $F$ on the 4-dimensional Abelian variety ${\bf A} = E_0^2 \times E_B^2$ , by $F = (\begin{matrix} \alpha & \hat{\phi}_B \\ -\phi_B & \hat{\alpha} \end{matrix})$ . The dual isogeny is $\hat{F} = (\begin{matrix} \hat{\alpha} & -\hat{\phi}_B \\ \phi_B & \alpha \end{matrix})$ and one can check $\hat{F} F = (c + 3^b) I_4 = 2^a I_4$ where $I_4$ is the identity map (or identity matrix if you want to view these as matrices).

Now, from the auxiliary points in SIDH we know how $\phi_B$ acts on $E_0[ 2^a ]$ . Since $\hat{\phi}_B \phi_B = [ 3^b]$ we can also compute how $\hat{\phi}_B$ acts on $E_B[ 2^a ]$ . Hence we can compute how $F$ acts on ${\bf A}[2^a]$ . Since $\ker(F) \subseteq {\bf A}[2^a]$ it means we compute $\ker(F)$ .

Now, knowing $\ker(F)$ we can use fancy methods to compute isogenies on high-dimensional Abelian varieties (and Damien Robert is a leading expert on this topic) and hence compute $F$ on any point. So, we compute $F$ on a basis for ${\bf A}[ 3^b]$ and hence compute $\phi_B$ on $E_0[ 3^b]$ and break SIDH.

The full attack works with an 8-dimensional Abelian variety ${\bf A} = E_0^4 \times E_B^4$ . I am not aware of any implementation of the attack as yet, but I look forward to seeing one. The attack can also be set up to compute the isogeny $\phi_A$ instead, simply by brute-forcing an extra small 3-power isogeny so that $3^b > 2^a$ .

As with my earlier blog post, I want to emphasise that this attack is only possible due to decades of research on computing isogenies of general Abelian varieties. This work was not primarily motivated by cryptographic applications but by the drive to generalization in pure mathematics.

— Steven Galbraith

Posted in Uncategorized | Leave a comment

Breaking supersingular isogeny Diffie-Hellman (SIDH)

Posted on July 31, 2022 by ellipticnews

The paper An efficient key recovery attack on SIDH by Wouter Castryck and Thomas Decru is a major breakthrough in isogeny cryptanalysis. This relates to the SIDH protocol by Jao and De Feo, and the NIST round 4 finalist SIKE.

I do not have time to explain all the technical details, but here are some quick answers to your burning questions.

Is the result true?

There is no reason to doubt this. Code is provided (though I haven’t run it myself) and I understand the SIKE team has confirmed the attack. Having solved the Microsoft $IKEp217 challenge, Castryck and Decru are eligible to claim the $50,000 USD prize.

Some aspects of the attack and its complexity analysis are heuristic, but that is normal and acceptable for cryptanalysis. The experimental results show that the attack is very practical.

How does the attack work?

The attack exploits the fact that SIDH has auxiliary points and that the degree of the secret isogeny is known. The auxiliary points in SIDH have always been an annoyance and a potential weakness, and they have been exploited for fault attacks, the GPST adaptive attack, torsion point attacks, etc.

Let $E_0$ be the base curve and let $P_0, Q_0 \in E_0$ have order $2^a$ . Let $E, P, Q$ be given such that there exists an isogeny $\phi$ of degree $3^b$ with $\phi : E_0 \to E$ , $\phi(P_0) = P$ , and $\phi(Q_0) = Q.$

A key aspect of SIDH is that one does not compute $\phi$ directly, but as a composition of isogenies of degree 3. In other words, there is a sequence of curves $E_0 \to E_1 \to E_2 \to \cdots \to E$ connected by 3-isogenies.

Essentially, like in GPST, the attack determines the intermediate curves $E_i$ and hence eventually determines the private key. At step $i$ the attack does a brute-force search of all possible $E_i \to E_{i+1}$ , and the magic ingredient is a gadget that shows which one is correct.

(The above is over-simplified, the isogenies $E_i \to E_{i+1}$ in the attack are not of degree 3 but of degree a small power of 3.)

What is this magic ingredient?

It is a theorem by Ernst Kani about reducible subgroups of abelian surfaces.

Is there a simple way to explain the magic ingredient?

Nope. Go learn about Richelot isogenies and abelian surfaces.

What does this mean for the NIST round 4 candidate SIKE?

The scheme specified in the SIKE NIST submission is broken.

Can SIDH be fixed?

Already on twitter there were several suggestions on how to possibly avoid the attack. For example, follow Peter Kutas @kutasp and Boris Fouotsa @FouotsaB for some threads.

To be able to use the magic ingredient the attacker must efficiently compute a number of isogenies with degrees of the form $2^i-3^j$ for various $1 \le i \le a, 1 \le j \le b$ and it is not clear how to do this if we are not close to a curve with small discriminant complex multiplication. So one hope is that SIDH can be saved by choosing a base curve $E_0$ with unknown endomorphism ring (this might require some kind of public setup).

The paper suggests that variants of SIDH such as B-SIDH (using primes other than 2 and 3) should be attackable. So it seems that changing the primes will not prevent the attack.

Does it break CSIDH or other isogeny cryptosystems?

No. The attack very specifically relies on two things: (1) that the degree of the secret isogeny is known; (2) the attacker is provided with the auxiliary points. Hence the attack does not seem to break CSIDH or SQISign.

Does it break ECC?

No. The attack assumes the degree of the isogeny is known, and that is exactly the secret key in ECC. There is no particular reason to think attacks on SIDH lead to attacks on ECC.

Why was it only discovered now?

The theoretical foundations of the attack are described in a paper by Kani from 1997 (and also some useful tools are in a paper by Howe, Leprévost and Poonen from 2000). So in some sense the attack could have been noticed at any time. But a key point is that this is not an attack one is going to discover by thinking only about isogenies between elliptic curves. The attack deeply exploits Richelot isogenies and products of elliptic curves and I doubt the attack can be expressed meaningfully without that language. This is the power of generalisation and extension. So what was necessary to find the attack was to have a community of scholars studying “esoteric” subjects like extending isogeny crypto to abelian surfaces.

Implications for PQ crypto

There is no doubt that this result will reduce confidence in isogenies. The sudden appearance of an attack this powerful shows that the field is not yet mature. The relatively recent attack by Ward Beullens on Rainbow has a similar impact on multivariate crypto. The correct response to this is not to attempt to minimise the impact, nor to reflexively declare the subject dead. Instead, we should keep our minds open and let the mathematicians work out the implications, wherever they lead. Personally, I can’t wait to see what Wouter and Thomas and all the isogenists come up with next!

— Steven Galbraith

Posted in Uncategorized | Leave a comment

Hertzbleed Attack

Posted on June 14, 2022 by ellipticnews

I woke up to the news of a new form of timing-side-channel attack based on the dynamic frequency scaling of modern x86 processors. This is the Hertzbleed attack, which will be presented at the USENIX Security Symposium in Boston in August. The authors are Yingchen Wang and Hovav Shacham from the University of Texas at Austin, Riccardo Paccagnella and Elizabeth Tang He and Christopher Fletcher from the University of Illinois Urbana-Champaign, and David Kohlbrenner from the University of Washington.

Interestingly for this blog, they target the supersingular isogeny key exchange protocol SIKE. SIKE is implemented in constant-time using standard timing-attack countermeasures from traditional ECC, such as the Montgomery ladder. But the frequency scaling feature allows to mount the timing attack even against supposedly constant-time code. The attack is a form of “zero value attack“. See also Patrick Longa’s comments on the NIST PQC mailing list.

The key property of SIKE that is exploited is that the protocol message is a triple $(E,P,Q)$ where $E$ is an elliptic curve and $P,Q$ are points. The points $P,Q$ are a troublesome aspect of SIDH/SIKE, and are the cause of the adaptive attack by Galbraith-Petit-Ti-Shani, the torsion point attacks by Petit and de Quehen-Kutas-Leonardi-Martindale-Panny-Petit-Stange, and so on. In certain contexts, these attacks are prevented by the Fujisaki-Okamoto transform, but this doesn’t help in the context of side-channel attacks.

The specific attack on SIKE given by the Hertzbleed authors is also of this form. It involves maliciously choosing the points $P,Q$ in a key-dependent way to learn information. As explained by Patrick Longa in his post above, there is a countermeasure to such attacks.

What does this mean for ECC in general? At the moment the timing channel does not seem to be fine-grained enough to attack constant-time elliptic curve systems in use. The paper says:

“Despite its theoretical power, it is not obvious how to construct practical exploits through the frequency side channel. This is because DVFS updates depend on the aggregate power consumption over millions of CPU cycles and only reflect coarse-grained program behavior. Yet, we show … that some cryptographic primitives admit amplification of single key bit guesses into thousands of high- or low-power operations, enough to induce a measurable timing difference.”

But we know that attacks only get better. So it will be interesting and important to see if this approach can be used to attack current ECC systems in practice.

— Steven Galbraith

Posted in Uncategorized | Leave a comment

Eurocrypt 2021 – Zagreb, Zoom and Zulip

Posted on October 24, 2021 by ellipticnews

Eurocrypt 2021 was held as a hybrid conference, with some participants in-person in Zagreb and some online. I was one of the ones joining the conference by Zoom and Zulip. As always in this blog I focus on talks and news most relevant for elliptic curve fans.

For each accepted paper there was a short (20-30 minutes) video available in advance of the conference on the conference website, and also a short live Q&A session that is immortalised on the IACR youtube channel.

There were two invited talks:

Craig Gentry’s talk “A Decade (or So) of Fully Homomorphic Encryption” (FHE) gave an overview of work on FHE, the current main applications of it, and possible future directions. He listed privacy preserving genome association, neural nets, and private information retrieval as three major application areas. He classified FHE schemes into four “generations”, the fourth of which is the CKKS (Cheon, Kim, Kim, Song) approach to FHE for floating point numbers. He gave an abstract formulation of FHE based on the Rothblum generic approach and showed how this seems to inevitably leads to several of the main schemes. Several times he challenged the community to construct FHE schemes not based on lattice assumptions, stating his conviction that lattices and FHE are not “soulmates” (but he is not willing to die in duel over this).

Sarah Meiklejohn cleverly tricked the audience into attending a talk on blockchain by using the title “An Evolution of Models for Zero-Knowledge Proofs”. The talk covered a wide range of applications and aspects of zero knowledge proofs, in particular a detailed discussion of the dependence on a common random string (CRS) and various trust models relating to the generation of the CRS.

The papers “Non-Interactive Zero Knowledge from Sub-exponential DDH” by Jain and Jin, “On the (in)security of ROS” by Benhamouda, Lepoint, Loss, Orrù and Raykova, and “New Representations of the AES Key Schedule” by Leurent and Pernot, were chosen for the Best Paper Awards. The first of these explicitly mentions elliptic curves: They require the sub-exponential hardness of DDH, which is only plausible for (non-pairing) elliptic curves. The paper is about Statistical NIZK arguments and Zaps.

Moving on to the rest of the conference program, I mention the following papers.

“Analysing the HPKE Standard” by Alwen, Blanchet, Hauck, Kiltz, Lipp and Riepel. The paper introduces the notion of “nominal group” to handle groups of non-prime order (such as Curve25519 and Curve448).

“Compact, Efficient and UC-Secure Isogeny-Based Oblivious Transfer” by Lai, Delpech de Saint Guilhem, and me. The paper shows how a special property of CSIDH (that $(a * E)^t = a^{-1} * E^t$ ) can be used to construct a two-round oblivious transfer (OT) scheme. The paper has a fully UC-secure 3-round version. In the live Q&A session, Lai announced that the paper has a “fixable bug” that means the fully secure version requires 4 rounds. Keep an eye on eprint for an updated version.

“One-way functions and malleability oracles: Hidden shift attacks on isogeny-based protocols” by Kutas, Merz, Petit and Weitkämper. The aim of the paper is study a group action (one can also view it as being a variant of the hidden number problem) in the SIDH setting, so that the Kuperberg-type hidden shift quantum algorithm (as applies to CSIDH) can also be applied to SIDH. The paper shows how to implement this in the case of overstretched SIDH parameters. These overstretched SIDH parameters are already known to be broken due to an attack by Petit. The method of the paper currently has no impact on the security of SIDH.

“Pre-Computation Scheme of Window $\tau$ -NAF for Koblitz Curves Revisited” by Yu and Xu is about efficient discrete-log crypto using elliptic curves. Sadly there were technical problems during the live session and so Yu was unable to answer questions. Since $\tau$ -NAF window methods have been studied for decades one would not expect major progress, but this paper gives a substantial speedup over the previous state-of-the-art. This is done by giving improved operation counts for computing $P \pm Q$ on Kohel’s $\mu_4$ -model of elliptic curves, and by organising the precomputation stage for the window method more effectively. Combined, these methods allow to potentially go as far as windows of length $w=7$ .

“Sieving for twin smooth integers with solutions to the Prouhet-Tarry-Escott problem” by Costello, Meyer and Naehrig is about choosing primes suitable for efficient implementation of B-SIDH and SQI-Sign. The problem is to construct primes $p=2m+1$ such that $m$ and $m+1$ are very smooth.

“Delay Encryption” by Burdges and De Feo has the best pre-recoded video — Watch it now! (At least, the first 5 minutes.) The paper is about delay functions based on sequential computation of isogenies.

“On Bounded Distance Decoding with Predicate: Breaking the Lattice Barrier for the Hidden Number Problem” by Albrecht and Heninger. The paper is about lattice algorithms for bounded distance decoding (BDD) by reducing to unique-SVP using the embedding technique and then applying enumeration or sieving. The additional feature is the use of a predicate that identifies the unique desired solution. This predicate naturally arises in problems like the hidden number problem (HNP) where the hidden number is the solution to a instance of the ECDLP. The main motivation of the paper is side-channel attacks recovering ECDSA private signing keys from known nonce bits.

“Classical vs Quantum Random Oracles” by Yamakawa and Zhandry discussed separations between the random oracle model (ROM) and the quantum random oracle model (QROM). They show a signature scheme that is secure in the ROM but insecure in the QROM, but as is to often the case with separations it is an artifial scheme that outputs the private key when a query is made on a certain type of input. The paper then gives positive results on Fiat-Shamir signatures and Full-Domain-Hash signatures (and more).

The Rump Session was entertaining. For readers of this blog the most interesting announcement was about the solution to the $5000 $IKE challenge. The talk was given by Craig Costello, who is one of the founders of the challenge. The challenge was solved by Aleksei Udovenko and Giuseppe Vitto. Interestingly, their approach uses the classic meet-in-the-middle approach (as mentioned in the original SIDH paper by Jao and De Feo) rather than the van Oorschot and Wiener (vOW) approach. The classic meet-in-the-middle approach is a time-memory tradeoff and so requires very large storage, whereas the vOW method is a low storage random walk method (but with higher time complexity). A paper is now on eprint that explains the computation and a number of optimisations. The $50,000 challenge is still waiting to be claimed!

— Steven Galbraith

Posted in Uncategorized | Leave a comment

Report by Luca de Feo on the 3rd PQC Standardization Conference

Posted on June 12, 2021 by ellipticnews

The 3rd PQC Standardization Conference, organized by NIST, took place online from June 7 to 9, featuring a mix of live talks, pre-recorded talks, and panels. The oral exchanges were complemented by a text-based forum, provided by an app well known for its lack of end-to-end encryption, where some topics were eventually debated at length. Slides for the talks will be available in a few days, and video recordings in a few weeks. In the meantime, I will give a personal account of the conference based exclusively on my recollections. I took no notes, and I was often preparing or eating dinner at the same time, so nothing of what I will report should be taken as an established truth.

Kicking-off the conference, NIST gave some interesting bits of information on the status of the selection process and the future. The timeline for the 3rd round stays put: NIST expects to announce the selected standards sometimes between the end of 2021 and the beginning of 2022, as well as the alternates that will move to Round 4. Two announcements stirred more emotions in the audience: NIST reported on the difficulties of acquiring patents that are perceived to hinder standardization of some candidates, and specifically pointed to a statement recently published by CNRS (archived). Several researchers with links to French academia have already expressed their disappointment with CNRS’ strategy. The second was a confirmation of a possibility that NIST had already hinted at previously: roughly 6 months after the end of the 3rd round, NIST plans to reopen the process to submissions, specifically seeking to add more variety to signatures. The audience understood that NIST will not accept new KEM candidates in this phase. Given the recent progress in designing post-quantum signature schemes, including some that received accolades at AsiaCrypt, this announcement should interest the readers of this blog. In the same spirit, NIST doubled down on the possibility of standardizing SPHINCS+ at the end of the 3rd round.

Throughout the three days, each of the finalists and alternate finalists had a 15 minutes slot to present their updates for the 3rd round. In most cases, there were minimal or no updates. PicNic appears to be the most notable exception, with important changes to the structure of the LowMC block cipher. Rainbow and GeMSS had some explaining to do, in response to recent advances in cryptanalysis, and GeMSS had to drop some parameters. Vadim Lyubashevsky and Dan Bernstein possibly gave the most opinionated talks, I recommend watching both when they are available.

Several contributed talks reported on various aspects of post-quantum cryptography. Lattices had the greatest share, I especially enjoyed the talks by Thomas Espitau and Yu Yang on variants of Falcon… or maybe was it the excellent Château Latour I was having at the same time? I also enjoyed the “Applications” session, which opened my eyes on how difficult it is to put any of the PQC candidates in constrained environments such as smartcards and IoT.

Of particular interest to the readers of this blog should be the three contributed talks on isogeny-based cryptography:

Péter Kutas (joint work with Christophe Petit) gave an excellent, if somewhat time-constrained, survey talk on several different “torsion point attacks” against SIDH and variants, which have previously appeared in this blog. The take-away message is that SIDH, SIKE and B-SIDH are well protected against all of them, be it because of the Fujisaki–Okamoto transform, or because of their intrinsic limitations, but the broader space of generalizations of SIDH a cryptographer might imagine is somewhat limited by these attacks, as it has already been repeatedly shown. I would certainly like to see more research in this promising direction, which has applications beyond cryptanalysis.
Élise Tasso (joint work with Nadia El Mrabet, Simon Pontié and myself) presented an in-the-lab confirmation of a fault-injection attack on SIDH first proposed by Ti. The attack is alarmingly easy to mount (ok, we used equipment worth 40k€, but that’s only because we’re rich), but at the same time:
- It requires multiple repetitions of key generation with the same secret key, something that should never happen in a correct implementation of SIDH or SIKE;
- It appears to be difficult to exploit in presence of key compression;
- It has a countermeasure so simple and cheap, that it may as well be included by default in the reference code.

The old-timers of this blog will not be surprised to learn that the best talk of the conference was delivered by Craig Costello. In only 5 minutes, Craig pretended to use SageMath code to generate pairs of toy SIDH public keys (one for Alice, one for Bob), discard the secrets, and (clumsily fail to) upload the public keys to a GitHub repo. Then, he announced that Microsoft is offering $5,000 for the solution of the smaller instance, named $IKEp182, and $50, 000 for that of the larger instance, named $IKEp217. The prize money matches what the SIKE team estimates to be the material cost of breaking the instances, so think twice before reallocating your BitCoin mining resources.

If you believe this stunt, then be our guest and start cracking, but don’t come whining when some mysterious bounty catcher from Australia claims the big prize. For now, I can only observe that everybody seems to trust Microsoft and no one has even forked the GitHub repo (but, do you trust GitHub, anyway?). As a public service to the community, here is the SHA1 of the latest commit, dated June 9, 2021: 72dc1cb50d5a78fee605757e2f33043b2f36f9b4, and here is the SHA-512 of the contents of the repo (excluding .git and .gitignore), as of June 9:

$ git clone https://github.com/microsoft/SIKE-challenges
$ cd SIKE-challenges/
$ cat * | sha512sum
d2d6c6b7627a0cdbdfc98515f0e99c3387f08ce06196f767b65541442d36fd5978a49761f6c8e6c4704c87bad3629a604ad176517a966023780288cc2c1e3ae9 -

Anyway, the video recording will be available in a few days, and you will all get a chance to have a close look at Craig’s sleight of hand. Be on the watch for video stitching by “those cheeky devils at the NSA”!

— Luca de Feo

Posted in Uncategorized | Leave a comment

	Aurore Guillevic on SIAM Conference on Applied Alg…
	Stefano Tessaro on Equivalence between CDH and…
	ellipticnews on Equivalence between CDH and…
	Michele Orru on Equivalence between CDH and…
	Aurore Guillevic on CRYPTO 2020

ellipticnews

New cryptanalysis of M-SIDH isogeny cryptography

SIAM Conference on Applied Algebraic Geometry (AG23)

Some comments on the CSIDH group action

Equivalence between CDH and DLP

EdDSA standardized

Attacks on SIDH/SIKE

Breaking supersingular isogeny Diffie-Hellman (SIDH)

Hertzbleed Attack

Eurocrypt 2021 – Zagreb, Zoom and Zulip

Report by Luca de Feo on the 3rd PQC Standardization Conference

Recent Posts

Recent Comments

Archives

Categories

Meta